|
|
|
|
|
|
|
|
Before we are done with this lesson we will have seen how we can view Newton's laws in a different way which allows us to see relationships which were hidden before. We will also learn about impulse and momentum and the importance of conservation principles.
This lesson begins the rapid expansion of scientific understanding as the Newtonian paradigm was applied in new ways to new situations.
It is not that momentum is significant in and of itself which concerns us. It is that the concept of conservation, specifically the fact that Newton's laws are axiomatic and can be viewed from a different perspective. It is also significant that we can view the physical universe in such an abstract, yet also quantitative way.
Momentum is only one of several physical quantities which is conserved. In this lesson we will see how this works in several situations and set the stage for our understanding of work and energy in the next lesson.
The problem with the swinging balls is that there is no explanation that can adequately describe their behavior. Aristotle would have been driven mad trying to give an animistic explanation.
We assume that the balls must follow Newton's laws, but it is difficult to see exactly how to apply them. We cannot easily measure the forces involved in the collison, nor can we measure the acceleration since it appears to be nearly instantaneous.
Watch the swinging balls
2.2.1. Are they intelligent balls which have been choreographed and rehearsed?
2.2.2. Are there special laws which apply only to these balls?
2.2.3. Is their behavior consistent with Newton's laws?2.2.3.1. if not then laws are incorrect or incomplete
2.3.1. cannot measure forces exchanged between balls
2.3.2. cannot measure acceleration of balls as they are struck
2.3.3. velocity appears to be instantaneously acquired
Fortunately, Newton's laws are good laws, that is the are applicable in virtually any situation. We can go back to the laws and re-examine them, taking a new perspective. In doing so, we will develop an important new concept, that of a conservation law. This will turn out to serve us very well, although in practice, conservation of momentum will not have much use.

3.4.1. Law is fundamental, so it should apply regardless of viewing perspective
3.4.2. certain situations do not allow detailed knowledge of forces or acceleration3.4.2.1. collisions, explosions, ejections
3.4.2.2. difficult to measure forces (strength, direction, duration)
3.4.2.3. easier to measure velocities and/or masses before and after
3.4.2.4. impulse can be determined if masses and change in velocity are known
3.4.2.5. force (magnitude, direction, duration) need not be known to predict outcome
When momentum is defined this way, as Newton defined it, "the quantity of motion", it becomes apparent that the force required to stop a moving mass depends on its momentum, not on the mass or the velocity alone.
4.3.1. "quantity of motion"
4.3.2. small object moving fast vs. large object moving slow
4.3.3. same mass at faster speeds requires more "something" to stop
4.3.4. that "something" is called impulse
Now it should be apparent that we do not need to know the acceleration in order to talk about forces. In fact, we do not even need to know the time involved in the force. What we do need to know is that a force applied over a time will cause a change in momentum. In fact, if the mass is constant (as it is in many cases) all we need to deal with is the change in velocity.
5.1.1. small force of long duration versus large force of short duration
5.1.2. Falling into thick foam pad vs. falling onto concrete: Which is preferable?
5.1.3. Maximum impulse is maximum force for maximum time
5.2.1. Equivalent to saying that rate of velocity change is proportional to force (if mass is constant)
5.2.2. allows for situations where mass is not constant5.2.2.1 rocket thrust where mass is expelled
5.2.2.2.other examples of changing mass?
Now we are ready to approach the idea of conservation. By this we do not mean "conserve" as "to use sparingly". In this context "conservation" means that something remains unchanged. In this section we will explore that concept and its applications in physics.
6.1.1. constancy amid change
6.1.2. a type of symmetry
6.2.1. momentum conservation combines second and third laws
6.3.1. equal and opposite forces for same duration ==> equal and opposite impulse
6.3.2. equal and opposite impulse ==> equal and opposite momentum change
6.3.3. equal and opposite momentum change ==> one object loses, another gains equal amount
6.3.4. loss by one = gain by other ==> total amount is constant
6.4.1. The total amount of momentum in a closed system remains constant, but may be transferred from one object to another.
6.4.2. total momentum before = total momentum after

6.5.1. Jill has no money, Bill has ten dollars:
Total Money between Jill and Bill Before = 0 + $10.00
sum is $10.006.5.2. Bill gives Jill five dollars:
Total Money between Jill and Bill After = $5.00 + 5.00
sum is $10.006.5.3. No matter how Jill and Bill distribute money among themselves, the total is $10.00
loss of one is gain by the other
closed system if neither spend nor acquire money
6.6.1. cart A has 10 N*s momentum, cart B has 0 momentum
total momentum between cart A and cart B = 0 + 10 n*s
p = 10 N*s
actual speed of cart A depends on its mass for a given amount of momentum
6.6.2. cart A and cart B collide, some momentum is transferred to cart B
loss by cart A = gain by cart B
total momentum between cart A and cart B is still 10 N*s6.6.3. actual speed after collision depends upon amount of momentum transferred and masses of carts
6.6.3.1. if masses are equal then speeds will be equal
6.7.1. recoil
cannon and cannonball have equal but opposite changes in momentur
"backwards" momentum of cannon equals "forward" momentum of cannonball
Mv + mV = 06.7.2. ballistic cart
used to measure velocities of small projectiles
mV = (M + m)v
momentum of bullet before collision = momentum of bullet and cart after collision6.7.3. elastic vs. inelastic collisions
6.7.3.1 inelastic collision
6.7.3.2 elastic collision
6.7.3.2.1 objects completely bounce off one another with no sticking at all
6.7.3.2.2 move at right angles after collision if masses are equal
6.7.3.2.3 more later in energy conservation
6.7.4. car crashes
6.7.4.1.can determine relative speed of two cars by direction of skidding after collision
6.7.5. atomic particles
6.7.5.1. tracks left by colliding atomic particles can be used to find the mass of the particles
6.8. Need to know initial speeds and masses of both carts, final speed of one cart to predict motion of the other
6.8.1. forces are exchanged, acceleration and deceleration is involved, but not necessary to know their magnitudes
6.8.2. is often impossible to know the details of forces and accelerations
6.8.3. conservation of energy is needed to know final state of both objects from initial conditions
Although conservation of momentum has only limited practical usefulness, if any in our everyday world, it is important to our study of the heritage of ideas for several reasons.
7.1.1. usually where forces are complex, or many objects involved
7.2.1. Modern physics describes the universe in terms of particles, forces and conservation
7.3.1. symmetry means unchanged with some kind of operations
7.3.2. conservation means something is unchanged upon interaction
Although our discussion so far has been limited to motion in one dimension, it is equaly applicable to motion in two or three dimensions. The video program shows several demonstrations of conservation of angular momentum. You might want to think about other applications in the world around you.
8.2.1. ANGULAR MOMENTUM: L = mvr
8.4.1. See the demonstrations in the video program
8.4.1.1. multidumbell
8.4.1.2. spinning wheel8.4.2. ice skaters, divers, cats land on feet, collapsing stars spin faster
8.4.3. Kepler's Laws8.4.3.1 planet moves faster when nearer to sun
8.4.3.2 when r is small, v must be proportionately large
Now we are ready to go back to the swinging balls and examine their behavior in light of our conservation law.
We will see that, although conservation can be used to partially explain their behavior, it is not sufficient in and of itself to explain it completely. For that we will need to understand conservation of energy, the topic of the next program.

9.1.1. total momentum before collision: mv = 0+0+0+0+mv
9.1.2. total momentum after collision: mv = mv+0+0+0+0
9.3.1. 2 balls in, 1 ball out at twice the speed
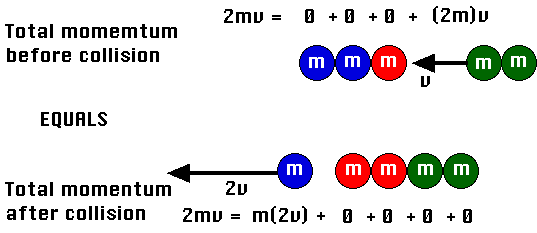
9.3.1.1. momemtum before collision: 2mv = 0+0+0+(2m)v
9.3.1.2. momentum after collision: 2mv = m(2v)+0+0+0+0
9.3.1.3. momentum is conserved9.3.2. 2 balls in, 4 balls out at half the speed

9.3.2.1. momentum before collision: 2mv = 0+0+0+(2m)v
9.3.2.2. momentum after collision 2mv = (4m)(.5v)+0
9.3.2.3. momentum is conserved
9.4.1. these other situations never occur so there must be some other principle besides conservation of momentum which determines their behavior.
9.5.1.
In this lesson we have seen how Newton's laws can be viewed from another perspective to understand the behavior of matter in situations where the forces and accelerations are unspecified or unmeasurable.
We saw howthe concept of conservation of momentum is related to symmetry, and how it can predict the behavior of many kinds of interactions, from collisions and explosions, to the motion of the planets in their elliptical orbits.
We also saw that conservation of momentum alone is necessary but not sufficient to explain the behavior of the "swinging balls."
In future programs we will rely heavily on the conservation concept as it has become one of the central concepts in all of physical science.